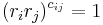Reflection group

For the Reflection Group On the Future of Europe, see European Council.

In group theory and geometry, a reflection group is a discrete group which is generated by a set of reflections of a finite-dimensional Euclidean space. The symmetry group of a regular polytope or of a tiling of the Euclidean space by congruent copies of a regular polytope is necessarily a reflection group. Reflection groups also include Weyl groups and crystallographic Coxeter groups. While the orthogonal group is generated by reflections (by the Cartan–Dieudonné theorem), it is a continuous group (indeed, Lie group), not a discrete group, and is generally considered separately.

1 Definition
2 Examples
- 2.1 Plane
- 2.2 Space
3 Kaleidoscopes
4 Relation with Coxeter groups
5 Finite fields
6 Generalizations
7 See also
8 References
9 External links

Definition

Let E be a finite-dimensional Euclidean space. finite reflection group is a subgroup of the general linear group of E which is generated by a set of orthogonal reflections across hyperplanes passing through the origin. An affine reflection group is a discrete subgroup of the affine group of E that is generated by a set of affine reflections of E (without the requirement that the reflection hyperplanes pass through the origin).

The corresponding notions can be defined over other fields, leading to complex reflection groups and analogues of reflection groups over a finite field.

Examples

Plane

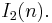In two dimensions, the finite reflection groups are the dihedral groups, which are generated by reflection in two lines that form an angle of $2\pi/n$ and correspond to the Coxeter diagram $I_2(n).$ Conversely, the cyclic point groups in two dimensions are not generated by reflections, and indeed contain no reflections – they are however subgroups of index 2 of a dihedral group.

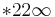Infinite reflection groups include the frieze groups $*\infty\infty$ and $*22\infty$ and the wallpaper groups 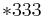$**$ , $*2222$ , $*333$ , $*442$ and $*632$ . If the angle between two lines is an irrational multiple of pi, the group generated by reflections in these lines is infinite and non-discrete, hence, it is not a reflection group.

Space

Finite reflection groups are the point groups C_nv, D_nh, and the symmetry groups of the five Platonic solids. Dual regular polyhedra (cube and octahedron, as well as dodecahedron and icosahedron) give rise to isomorphic symmetry groups. The classification of finite reflection groups of R³ is an instance of the ADE classification.

Kaleidoscopes

Reflection groups have deep relations with kaleidoscopes, as discussed in (Goodman 2004).

Relation with Coxeter groups

A reflection group W admits a presentation of a special kind discovered and studied by H.S.M. Coxeter. The reflections in the faces of a fixed fundamental "chamber" are generators r_i of W of order 2. All relations between them formally follow from the relations

$(r_i r_j)^{c_{ij}}=1$

expressing the fact that the product of the reflections r_i and r_j in two hyperplanes H_i and H_j meeting at an angle 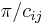$\pi/c_{ij}$ is a rotation by the angle 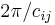$2\pi/c_{ij}$ fixing the subspace H_i ∩ H_j of codimension 2. Thus, viewed as an abstract group, every reflection group is a Coxeter group.

Finite fields

When working over finite fields, one defines a "reflection" as a map that fixes a hyperplane (otherwise for example there would be no reflections in characteristic 2, as $-1=1$ so reflections are the identity). Geometrically, this amounts to including shears in a hyperplane. In characteristic 2, using the above fixed-hyperplane definition of "reflection," it is no longer true that every finite reflection group is a Coxeter group. See A simple reflection group of order 168. Reflection groups over finite fields of characteristic not 2 were classified in (Zalesskiĭ & Serežkin 1981).

Generalizations

Discrete isometry groups of more general Riemannian manifolds generated by reflections have also been considered. The most important class arises from Riemannian symmetric spaces of rank 1: the n-sphere Sⁿ, corresponding to finite reflection groups, the Euclidean space Rⁿ, corresponding to affine reflection groups, and the hyperbolic space Hⁿ, where the corresponding groups are called hyperbolic reflection groups. In two dimensions, triangle groups include reflection groups of all three kinds.

References

Standard references include (Humphreys 1992) and (Grove & Benson 1996).

Coxeter, H.S.M. (1934), "Discrete groups generated by reflections", Ann. of Math. 35: 588–621
Coxeter, H.S.M. (1935), "The complete enumeration of finite groups of the form 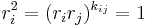$r_i^2=(r_ir_j)^{k_{ij}}=1$ ", J. London Math. Soc. 10: 21–25
Goodman, Roe (April 2004), "The Mathematics of Mirrors and Kaleidoscopes", American Mathematical Monthly, http://www.math.rutgers.edu/~goodman/pub/monthly.pdf
Humphreys, James E. (1992), Reflection groups and Coxeter groups, Cambridge University Press, ISBN 978-0-521-43613-7
Zalesskiĭ, A E; Serežkin, V N (1981), "Finite Linear Groups Generated by Reflections", Math. USSR Izv. 17 (3): 477–503, doi:10.1070/IM1981v017n03ABEH001369
Kane, Richard, Reflection groups and invariant theory (review), http://www.cms.math.ca/Publications/Reviews/2003/rev4.pdf
Hartmann, Julia; Shepler, Anne V., Jacobians of reflection groups, arXiv:math/0405135
Dolgachev, Igor V., Reflection groups in algebraic geometry, arXiv:math.AG/0610938

External links

E. B. Vinberg (2001), "Reflection group", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=R/r080520